13.4 Latent-data formulation

• Alternate formulation using a continuous ‘latent’ variable \(z_i\). It is completely equivalent to the logistic regression.

• ‘latent’ means unobserved

$$ \[\begin{align} y_i &= \begin{cases} 1 & \text{if } z_i > 0 \\ 0 &\text{if } z_i < 0 \\ \end{cases} \\ z_i &= X_i\beta + \epsilon_i \end{align}\] $$

Here the \(\epsilon_i\) are independent and have the logistic distribution:

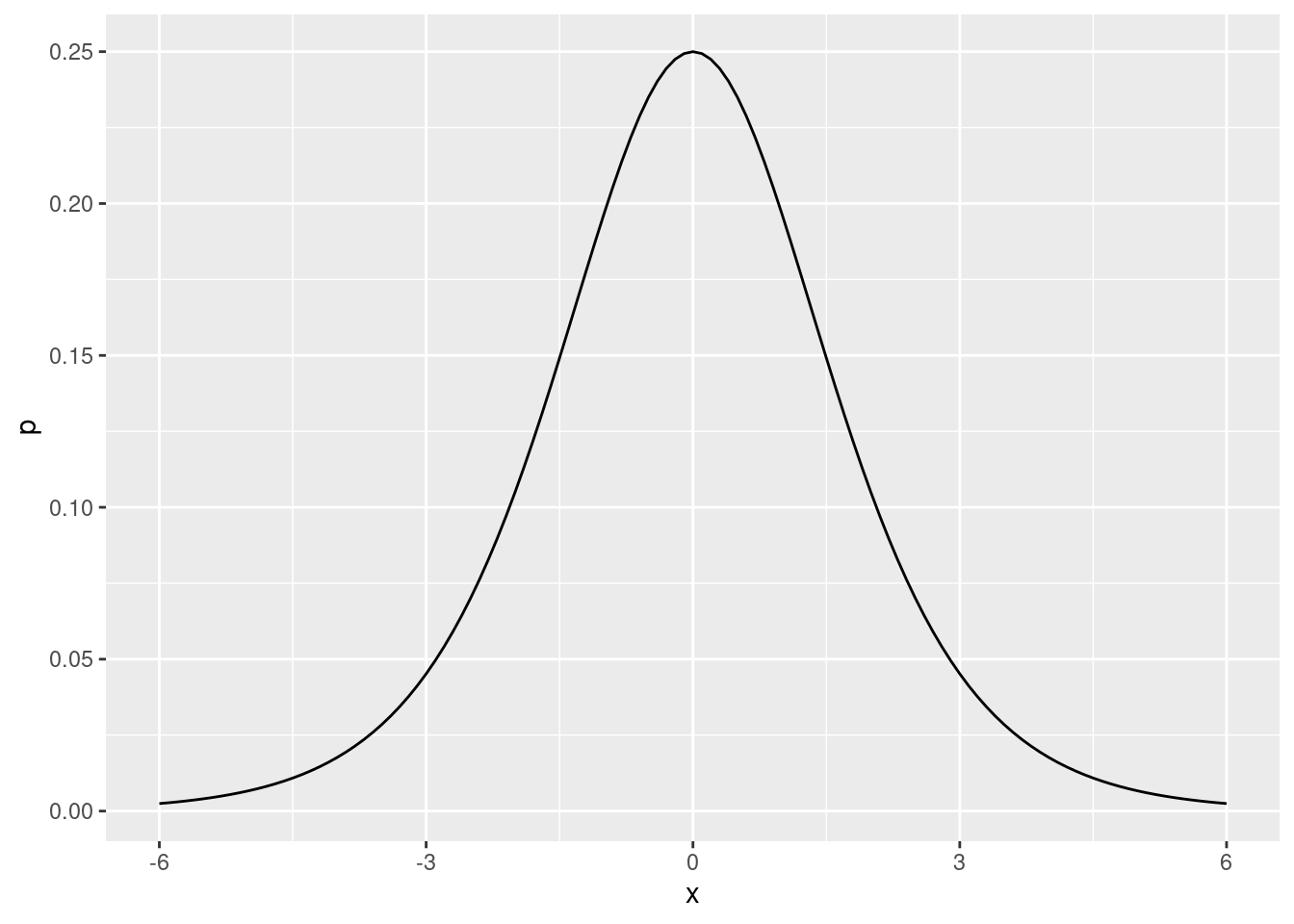
• The distribution of the error terms is similar to a Gaussian with \(\sigma = 1.6\). What we relaxed that and use a Gaussian fit \(\sigma\) ?

• Answer: It wont work because the ‘latent’ scale parameter \(\sigma\) is non-identifiable. You can pick any $you want and you can get the same predictions by scaling the slope and intercept!

• So why bother?

  • In some settings direct information is available for the \(z_i\)’s

  • We will see in later chapters this latent formulation can be useful.