16.2 General Principles of design (proportions)

• Sample size to achieve a specified standard error:

  • Standard error: $\sqrt{p(1-p)/n} \approx 0.5/\sqrt{n}$
  • So $n \approx (0.5/\text{s.e.})^2$

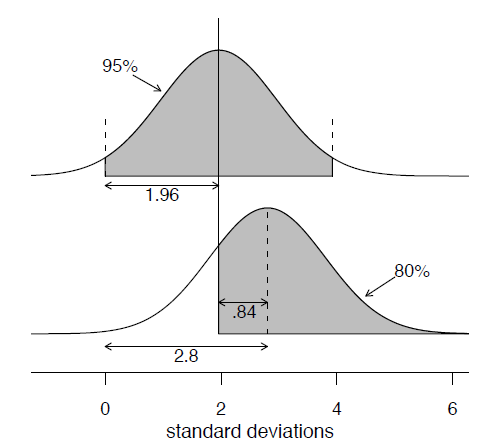
• Sample size to achieve specified probability (power) of statistical significance:

  • For 80% probabilty of 95% statistical significance, the true effect must be 2.8 standard errors from zero
  • $n = p(1-p)(2.8/(p-p_0))^2$

• For comparisons of proportions, you need approximately 4 times the samples.