5.3 Standardized incidence ratio

Estimation of the disease risk estimates in each of the areas

\[SIR_i=\frac{Y_i}{E_i}\] \(E_i\) is the expected counts or the expected total number of cases, is the sum of the multiplication of the rate of the number of cases divided by population in \(j\) \(r_j^{(s)}\), and \(n_j^{(i)}\) the population in stratum \(j\) of area \(i\).

\[E_i=\sum_{j=1}^m{r_{j}^{(s)}n_{j}^{(i)}}\]

\[SIR_i=\begin{Bmatrix} >1 & \text{higher} \\ =1 & \text{equal} \\ <1 & \text{lower} \end{Bmatrix} \text{risk than expected in area i}\]

When applied to mortality data, the ratio is known as the standardized mortality ratio (SMR).

Example:

d <- pennLC$data%>%
  group_by(county) %>% 
  summarize(Y = sum(cases))

head(d)

## # A tibble: 6 × 2
##   county        Y
##   <fct>     <int>
## 1 adams        55
## 2 allegheny  1275
## 3 armstrong    49
## 4 beaver      172
## 5 bedford      37
## 6 berks       308

pennLC$data <- pennLC$data %>%
  arrange(county,race,gender,age)

E <- expected(
  population = pennLC$data$population,
  cases = pennLC$data$cases, n.strata = 16
)

d$E <- E[match(d$county, unique(pennLC$data$county))]


head(d)

## # A tibble: 6 × 3
##   county        Y      E
##   <fct>     <int>  <dbl>
## 1 adams        55   69.6
## 2 allegheny  1275 1182. 
## 3 armstrong    49   67.6
## 4 beaver      172  173. 
## 5 bedford      37   44.2
## 6 berks       308  301.

d$SIR <- d$Y / d$E

head(d)

## # A tibble: 6 × 4
##   county        Y      E   SIR
##   <fct>     <int>  <dbl> <dbl>
## 1 adams        55   69.6 0.790
## 2 allegheny  1275 1182.  1.08 
## 3 armstrong    49   67.6 0.725
## 4 beaver      172  173.  0.997
## 5 bedford      37   44.2 0.837
## 6 berks       308  301.  1.02

map <- merge(map, d)

mapsf <- st_as_sf(map)

ggplot(mapsf) + geom_sf(aes(fill = SIR)) +
  scale_fill_gradient2(
    midpoint = 1, low = "blue", mid = "white", high = "red"
  ) +
  theme_bw()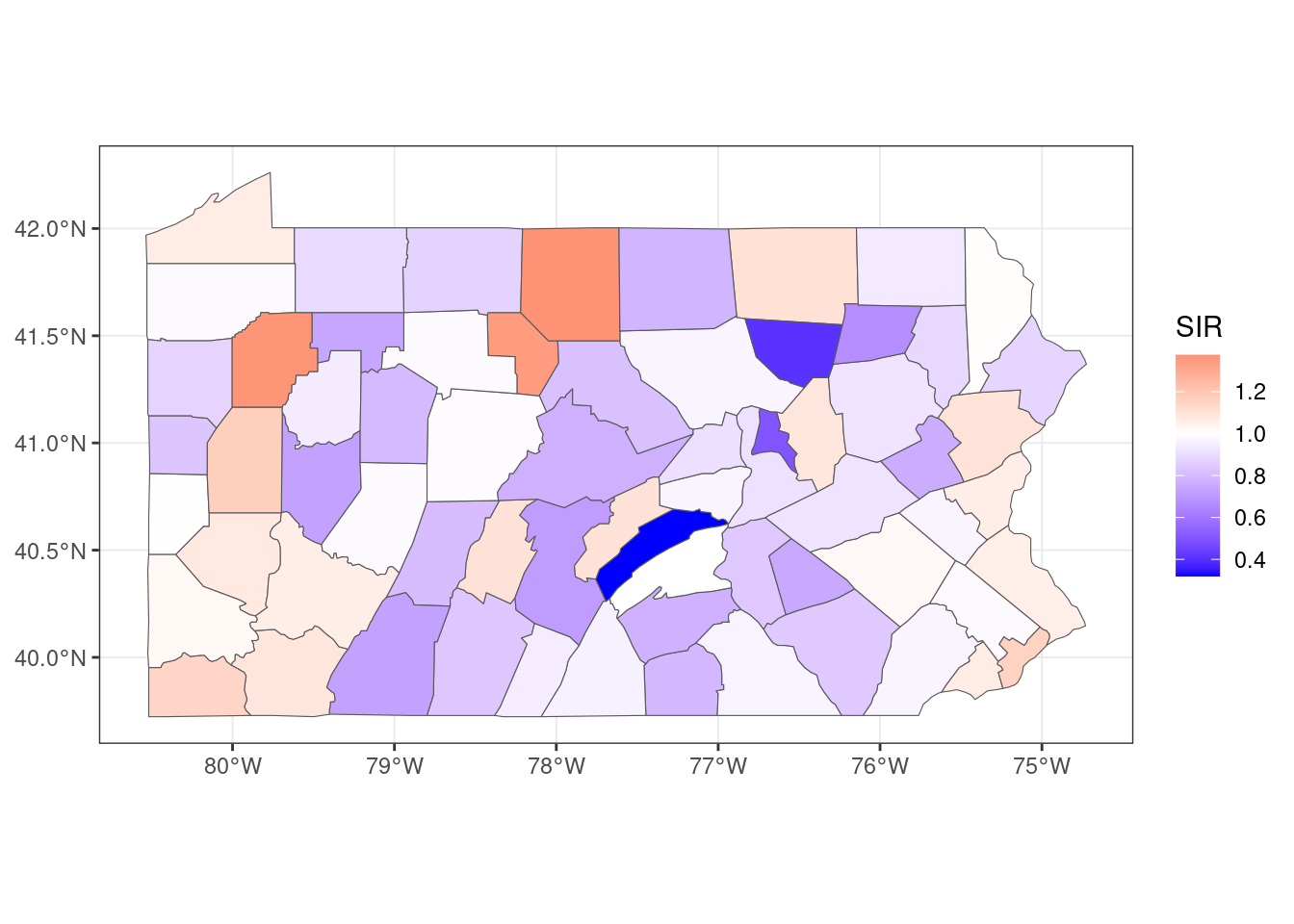

Figure 5.2: SIR of lung cancer in Pennsylvania counties