6.1 Crear un modelo

6.1.1 Diferentes Interfaces de Modelado

diferentes interfaces

• Interfaces de Modelado
  • Diferentes Implementaciones = Diferentes Interfaces
  • Regresión Lineal puede ser implementada en varias maneras
    • Mínimos Cuadrados Ordinarios (MCO) / Ordinary Least Squares
    • Regresión Lineal Regularizada / Regularized Linear Regression
    • …

• {stats}
  • toma una fórmula
  • usa un data.frame

lm(formula, data, ...)

• {glmnet}
  • tiene una interfaz x/y
  • usa una matriz

glmnet(x = matrix, y = vector, family = "gaussian", ...)

6.1.2 Especificación del Modelo

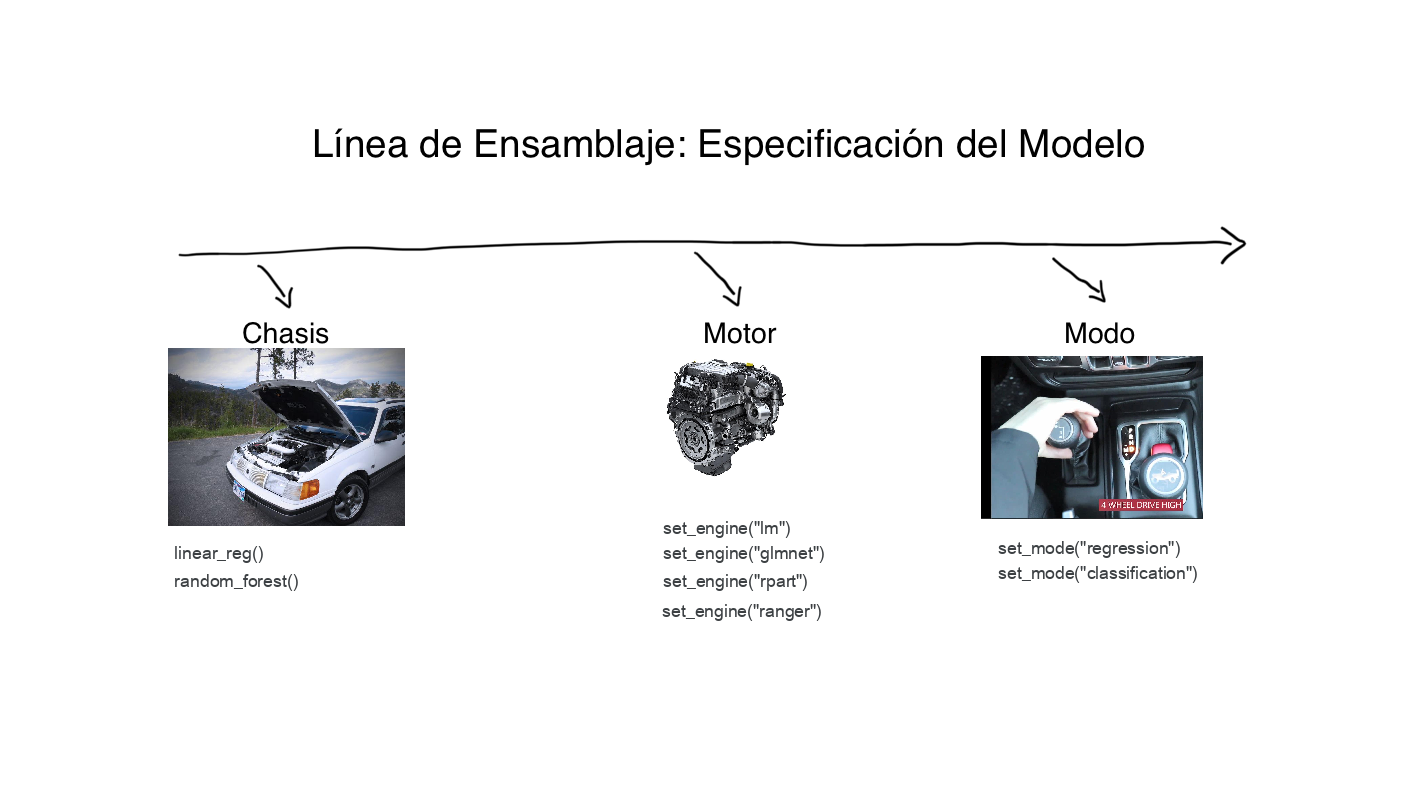
especificación del modelo

• {tidymodels}/{parsnip}
  • La idea es unificar y crear interfases más predecibles.
    • Especificar el tipo de modelo (e.g. regresión lineal, bosques aleatorios, …)
      • linear_reg()
      • rand_forest()
    • Especificar el “motor” (i.e. paquete con la implementación del algoritmo)
      • set_engine("paquete con la implementación")
    • Especificar el modo (e.g. clasificación vs regresión lineal)
      • usa esto cuando el modelo puede ejecutar ambas clasificación y regresión lineal
      • set_mode("regression")
      • set_mode("classification")

• Trayendo todo junto

lm_model_spec <- 
  parsnip::linear_reg() %>% # especificar el modelo
  parsnip::set_engine("lm") # especificar el motor


lm_model_spec

## Linear Regression Model Specification (regression)
## 
## Computational engine: lm

6.1.3 Ajustando el Modelo

Usando la especificación de modelo previamente definida

• fit()
  • cualquier variable nominal o categórica será separada en variables artificiales
  • la mayoría de métodos que usan una fórmula hacen esto mismo
• fit_xy
  • retrasa la creación de variables artificiales y tiene una función de modelo subyacente

# crear un ajuste de modelo usando una fórmula
lm_form_fit <- 
  lm_model_spec %>% 
  parsnip::fit(Sale_Price ~ Longitude + Latitude, data = ames_train)

# crear un ajuste de modelo usando x/y
lm_xy_fit <- 
  lm_model_spec %>% 
  parsnip::fit_xy(
    x = ames_train %>% dplyr::select(Longitude, Latitude),
    y = ames_train %>% dplyr::pull(Sale_Price)
  )

6.1.4 Argumentos de Modelo Generalizados

• Como las interfases de modelo que varian, los parámetros de los modelos también varian de implementación a implementación
• Dos niveles de argumentos de modelos
  • argumentos principales - Parámetros alineados con vehículos matemáticos
  • argumentos de motor - Parámetros alineados con el paquete de implementación del algoritmo matemático

argumento	ranger	randomForest	sparklyr
predictores muestreados	mtry	mtry	feature_subset_strategy
árboles	num.trees	ntree	num_trees
observaciones a separar	min.node.size	nodesize	min_instances_per_node

argumento	parsnip
predictores muestreados	mtry
árboles	trees
observaciones a separar	min_n

{parsnip} en acción

• La función translate() provee el mapeo desde la interfaz de {parsnip} a cada uno de los paquetes de implementación de los algoritmos.

# implementación de stats
parsnip::linear_reg() %>% 
  parsnip::set_engine("lm") %>% 
  parsnip::translate()

## Linear Regression Model Specification (regression)
## 
## Computational engine: lm 
## 
## Model fit template:
## stats::lm(formula = missing_arg(), data = missing_arg(), weights = missing_arg())

# implementación de glmnet
parsnip::linear_reg(penalty = 1) %>% 
  parsnip::set_engine("glmnet") %>% 
  parsnip::translate()

## Linear Regression Model Specification (regression)
## 
## Main Arguments:
##   penalty = 1
## 
## Computational engine: glmnet 
## 
## Model fit template:
## glmnet::glmnet(x = missing_arg(), y = missing_arg(), weights = missing_arg(), 
##     family = "gaussian")