5.3 Class imbalance
In many instances, random splitting is not suitable. This includes datasets that contain class imbalance, meaning one class is dominated by another. Class imbalance is important to detect and take into consideration in data splitting. Performing random splitting on a dataset with severe class imbalance may cause the model to perform badly at validation. You want to avoid allocating the minority class disproportionately into the training or test set. The point is to have the same distribution across the training and test sets. Class imbalance can occur in differing degrees:
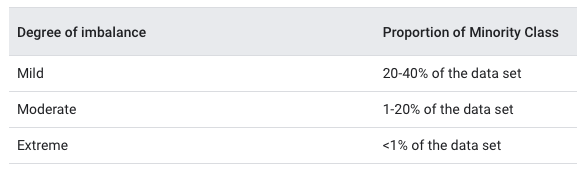
Splitting methods suited for datasets containing class imbalance should be considered. Let’s consider a #Tidytuesday dataset on Himalayan expedition members, which Julia Silge recently explored here using {tidymodels}.
library(tidyverse)
library(skimr)
members <- read_csv("https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2020/2020-09-22/members.csv")
skim(members)| Name | members |
| Number of rows | 76519 |
| Number of columns | 21 |
| _______________________ | |
| Column type frequency: | |
| character | 10 |
| logical | 6 |
| numeric | 5 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| expedition_id | 0 | 1.00 | 9 | 9 | 0 | 10350 | 0 |
| member_id | 0 | 1.00 | 12 | 12 | 0 | 76518 | 0 |
| peak_id | 0 | 1.00 | 4 | 4 | 0 | 391 | 0 |
| peak_name | 15 | 1.00 | 4 | 25 | 0 | 390 | 0 |
| season | 0 | 1.00 | 6 | 7 | 0 | 5 | 0 |
| sex | 2 | 1.00 | 1 | 1 | 0 | 2 | 0 |
| citizenship | 10 | 1.00 | 2 | 23 | 0 | 212 | 0 |
| expedition_role | 21 | 1.00 | 4 | 25 | 0 | 524 | 0 |
| death_cause | 75413 | 0.01 | 3 | 27 | 0 | 12 | 0 |
| injury_type | 74807 | 0.02 | 3 | 27 | 0 | 11 | 0 |
Variable type: logical
| skim_variable | n_missing | complete_rate | mean | count |
|---|---|---|---|---|
| hired | 0 | 1 | 0.21 | FAL: 60788, TRU: 15731 |
| success | 0 | 1 | 0.38 | FAL: 47320, TRU: 29199 |
| solo | 0 | 1 | 0.00 | FAL: 76398, TRU: 121 |
| oxygen_used | 0 | 1 | 0.24 | FAL: 58286, TRU: 18233 |
| died | 0 | 1 | 0.01 | FAL: 75413, TRU: 1106 |
| injured | 0 | 1 | 0.02 | FAL: 74806, TRU: 1713 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| year | 0 | 1.00 | 2000.36 | 14.78 | 1905 | 1991 | 2004 | 2012 | 2019 | ▁▁▁▃▇ |
| age | 3497 | 0.95 | 37.33 | 10.40 | 7 | 29 | 36 | 44 | 85 | ▁▇▅▁▁ |
| highpoint_metres | 21833 | 0.71 | 7470.68 | 1040.06 | 3800 | 6700 | 7400 | 8400 | 8850 | ▁▁▆▃▇ |
| death_height_metres | 75451 | 0.01 | 6592.85 | 1308.19 | 400 | 5800 | 6600 | 7550 | 8830 | ▁▁▂▇▆ |
| injury_height_metres | 75510 | 0.01 | 7049.91 | 1214.24 | 400 | 6200 | 7100 | 8000 | 8880 | ▁▁▂▇▇ |
Let’s say we were interested in predicting the likelihood of survival or death for an expedition member. It would be a good idea to check for class imbalance:
library(janitor)
members %>%
tabyl(died) %>%
adorn_totals("row")## died n percent
## FALSE 75413 0.98554607
## TRUE 1106 0.01445393
## Total 76519 1.00000000We can see that nearly 99% of people survive their expedition. This dataset would be ripe for a sampling technique adept at handling such extreme class imbalance. This technique is called stratified sampling, in which “the training/test split is conducted separately within each class and then these subsamples are combined into the overall training and test set”. Operationally, this is done by using the strata argument inside initial_split():
set.seed(123)
members_split <- initial_split(members, prop = 0.80, strata = died)
members_train <- training(members_split)
members_test <- testing(members_split)5.3.1 Stratified sampling simulation
With simulation we can see the effect of stratification: we expect that the expected value does not change with stratification but the variance is lower.
simulate_stratified_sampling <- function(prop_in_dataset, n_resample = 50,
n_rows = 1000, seed = 45678) {
set.seed(seed)
data_to_split <- tibble(died = c(
rep(1, floor(n_rows * prop_in_dataset)),
rep(0, floor(n_rows * (1 - prop_in_dataset)))
))
samples <- map_dfr(seq_len(n_resample), ~{
initial_split(data_to_split) %>%
testing() %>%
summarize(died_pct = mean(died))
})
stratified_samples <- map_dfr(seq_len(n_resample), ~{
initial_split(data_to_split, strata = died) %>%
testing() %>%
summarize(died_pct = mean(died))
})
rbind(
samples %>% mutate(stratified = FALSE),
stratified_samples %>% mutate(stratified = TRUE)
) %>%
group_by(stratified) %>%
summarize(mean = mean(died_pct), var = var(died_pct))
}rsample does not stratify if class imbalance is more extreme than 10%
simulate_stratified_sampling(0.09)## # A tibble: 2 × 3
## stratified mean var
## <lgl> <dbl> <dbl>
## 1 FALSE 0.0910 0.000240
## 2 TRUE 0.0917 0.000257Stratified sampling happens:
simulate_stratified_sampling(0.11)## # A tibble: 2 × 3
## stratified mean var
## <lgl> <dbl> <dbl>
## 1 FALSE 0.110 0.000257
## 2 TRUE 0.112 0