Exercise 3.1.7

Kepler found that the orbital period $\tau$ of a planet depends on its mean distance $R$ from the sun according to $\tau=c R^{\alpha}$ for a simple rational number $\alpha$. Perform a linear least-squares fit from the following table in order to determine the most likely simple rational value of $\alpha$.

tau = [87.99, 224.7, 365.26, 686.98, 4332.4, 10759, 30684, 60188];
R = [57.59, 108.11, 149.57, 227.84, 778.14, 1427, 2870.3, 4499.9];
scatter(R,tau,title="Orbital Period (days)", label = "data",
    xlabel=L"R (Mkm)",ylabel=L"tau")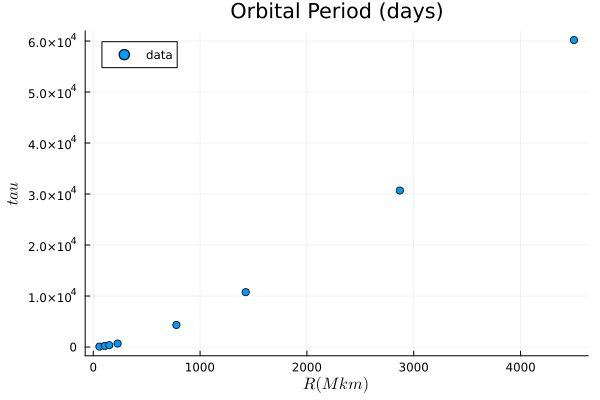

figure 4

Using the log-log transformation:

$$\log \tau = \log c + \alpha \log R$$

V = [R.^0 log.(R)];
c = V \ log.(tau);
@show c[2]

# c[2] = 1.4986486620150812

So the exponent is close to 3/2, which matches Keplar’s third law (usually expressed as $\tau^2 \propto R^3$)