An Optimization Classic

Example:

Rosenbrock function: A function of two variables with minimum at \((a,a^2)\), which lies inside a narrow valley:

\[ (a- x_1)^2 + b(x_2 - x_1^2)^2 \]

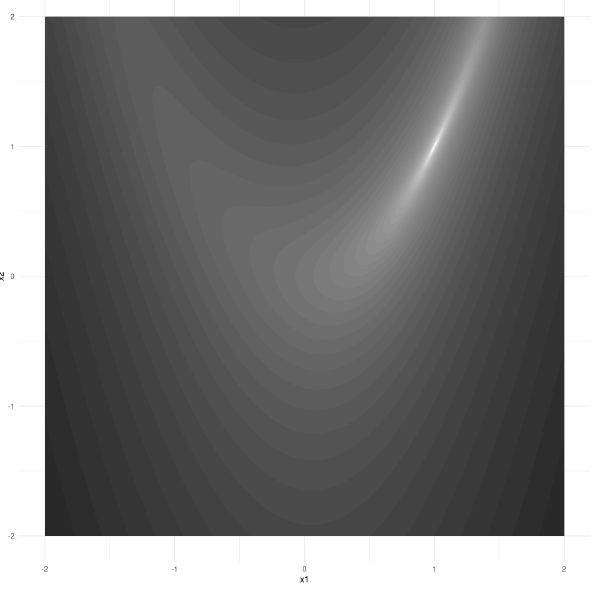
Below we set values for a and b and define the rosenbrock function. We expect the minimum of the function to be at \((1,1)\) (when a=1).

a <- 1
b <- 5

rosenbrock <- function(x){
  x1 <- x[1]
  x2 <- x[2]
  (a - x1)^2 + b * (x2 - x1^2)^2
}