20. Low-Rank Adapters (LoRA)

Learning objectives

  • Motivate dimension reduction
  • Discuss LoRA
  • Introduce DoRA

Low-Rank Adaptation

Palmer Penguins

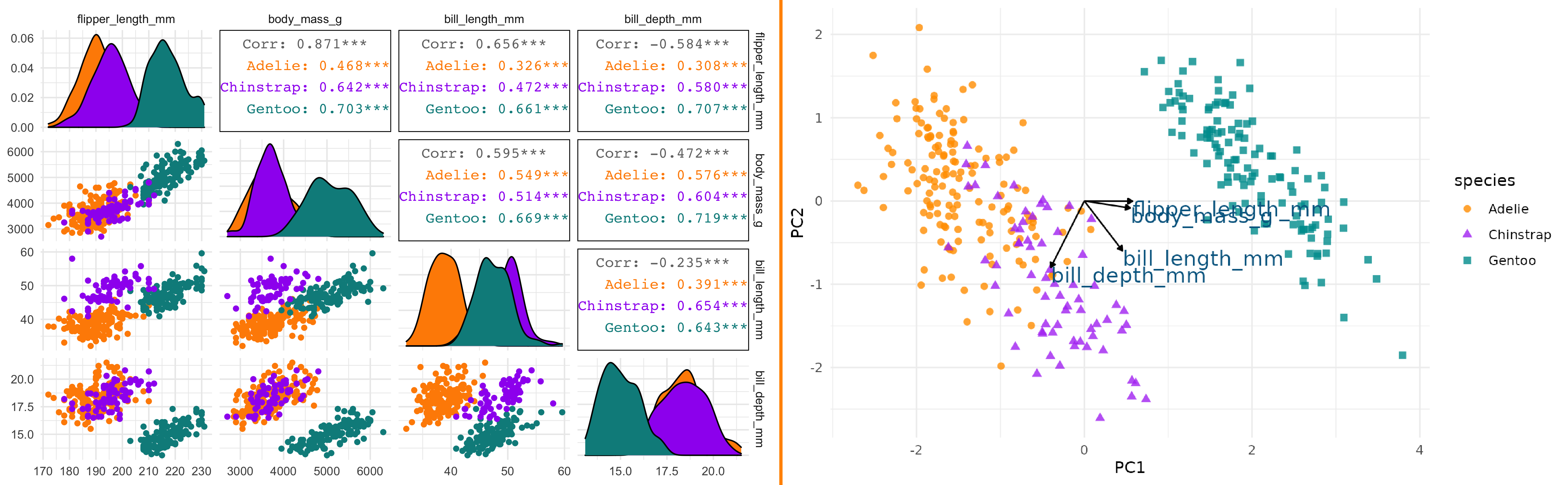
Allison Horst

SVD

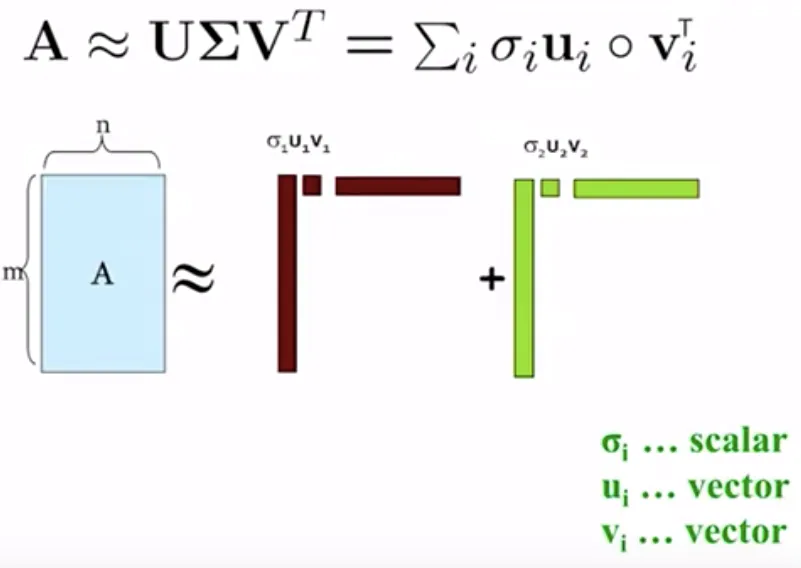
SVD

Update Rule

\[\begin{array}{rcl} W_{1} & = & W_{\text{pre}} + \Delta W_{0} \\ W_{2} & = & W_{1} + \Delta W_{1} \\ W_{3} & = & W_{2} + \Delta W_{2} \\ ... & ~ & ... \\ W_{\text{out}} \end{array}\]

Freezing the Pre-Training Weights

\[W_{\text{out}} = W_{\text{pre}} + \displaystyle\sum_{i = 0} \Delta W_{i}\]

Fine Tuning

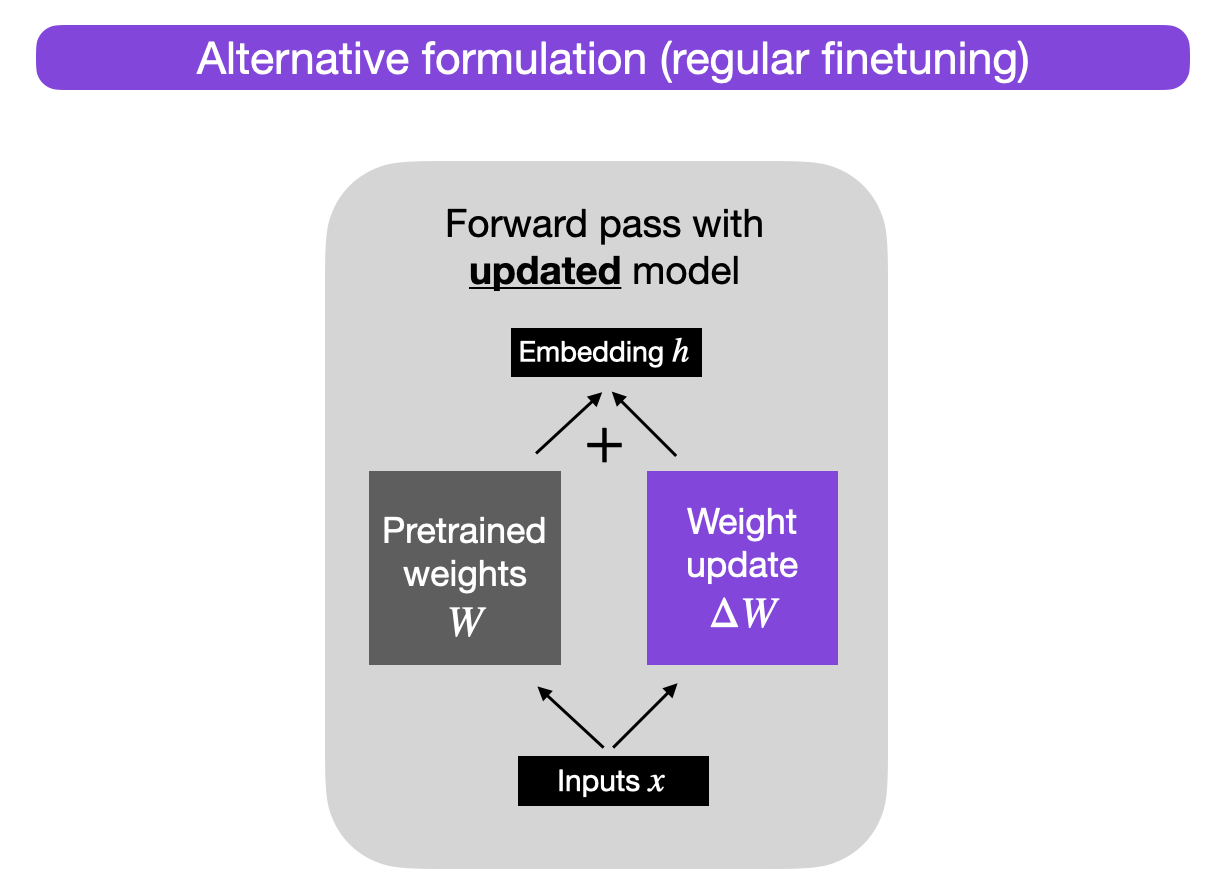
fine tuning scheme

Dimensionality Reduction

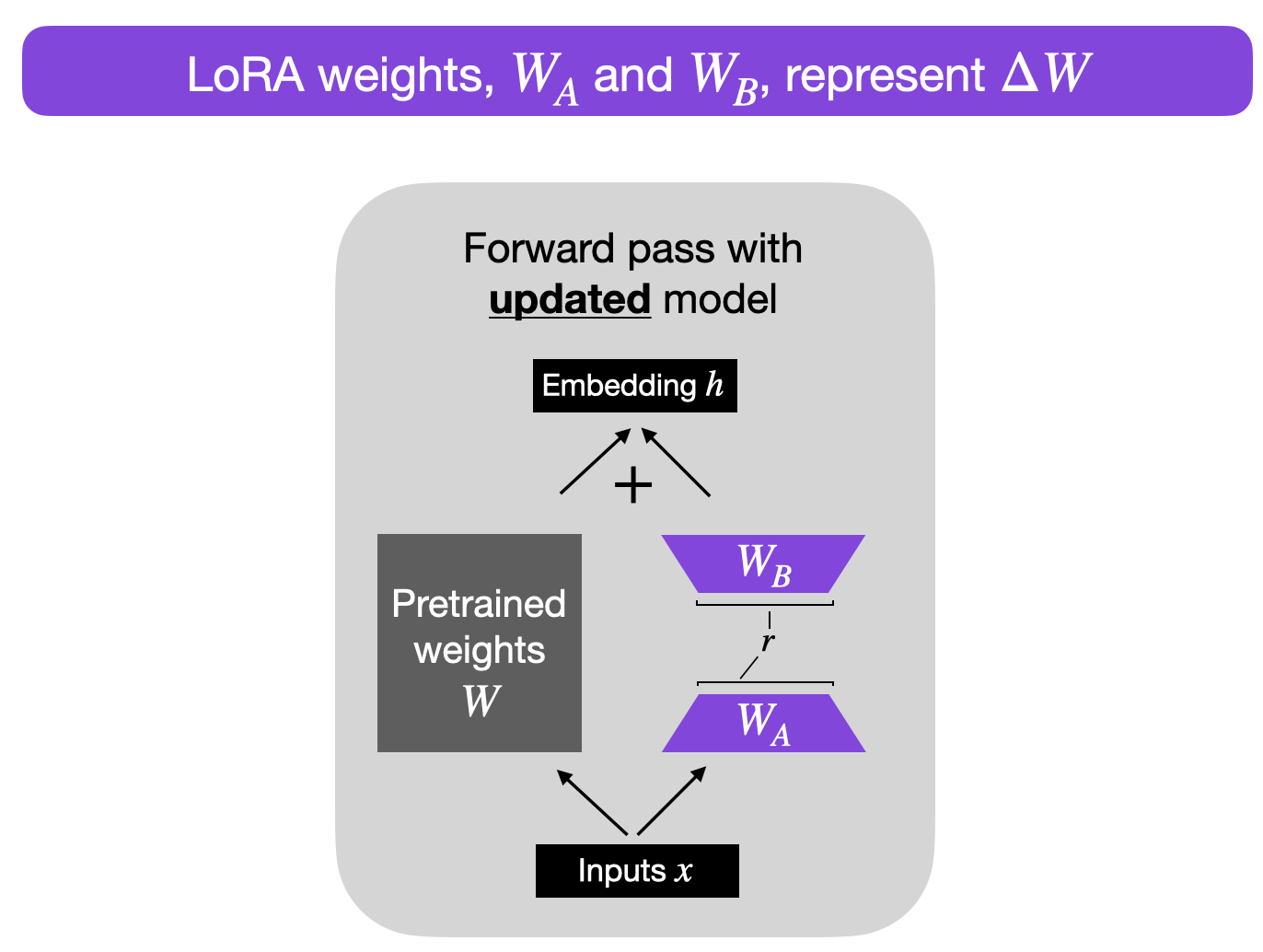
matrix factorization

Speed versus Complexity Trade-Off

  • smaller rank \(r\)

    • fewer parameters
    • faster training
    • lower compute

  • larger rank \(r\)

    • more likely to capture task-specific information

Demonstration

DoRA

DoRA from Vectors

Weight-Decomposed Low-Rank Adaptation

  • \(m\): magnitude vector
  • \(V\): directional matrix

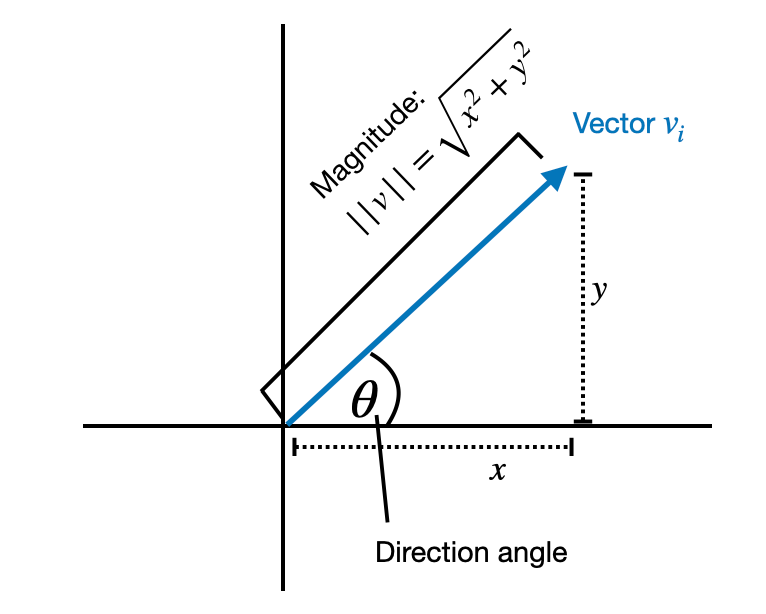
vectors!

DoRA Decomposition

\[W' = m \cdot \frac{W_{0} + BA}{||W_{0} + BA||_{c}}\]

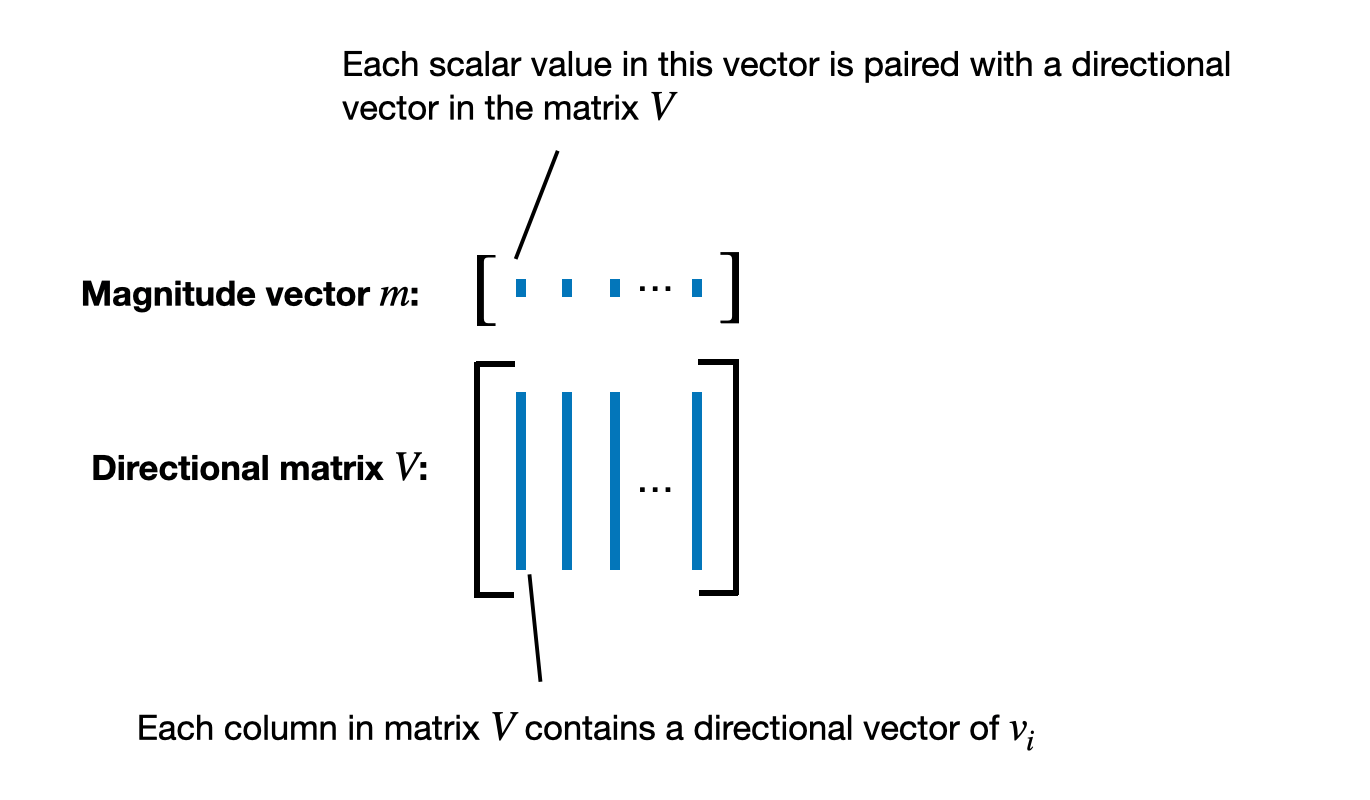
DoRA decomposition

DoRA Workflow

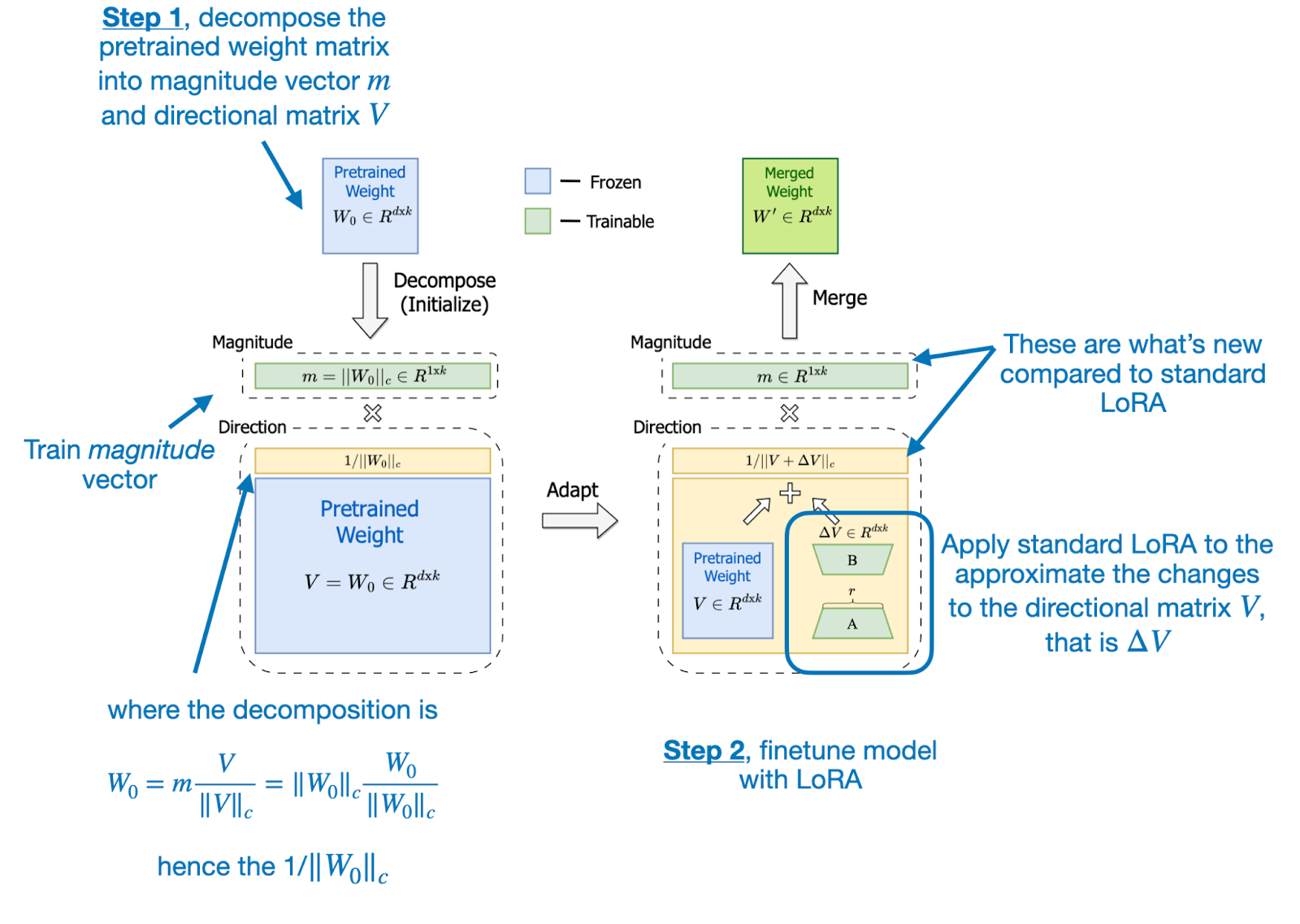
DoRA workflow