2. Statistical Prediction and Supervised Learning
Learning objectives
Statistics and Probability
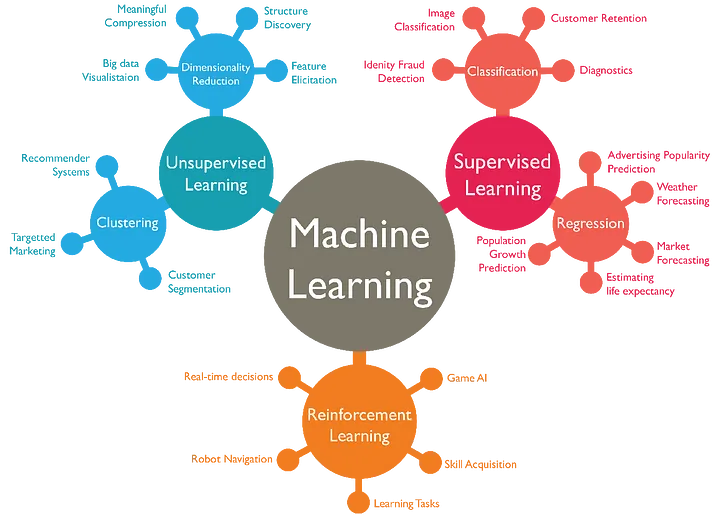
Machine Learning
Regression vs Classification
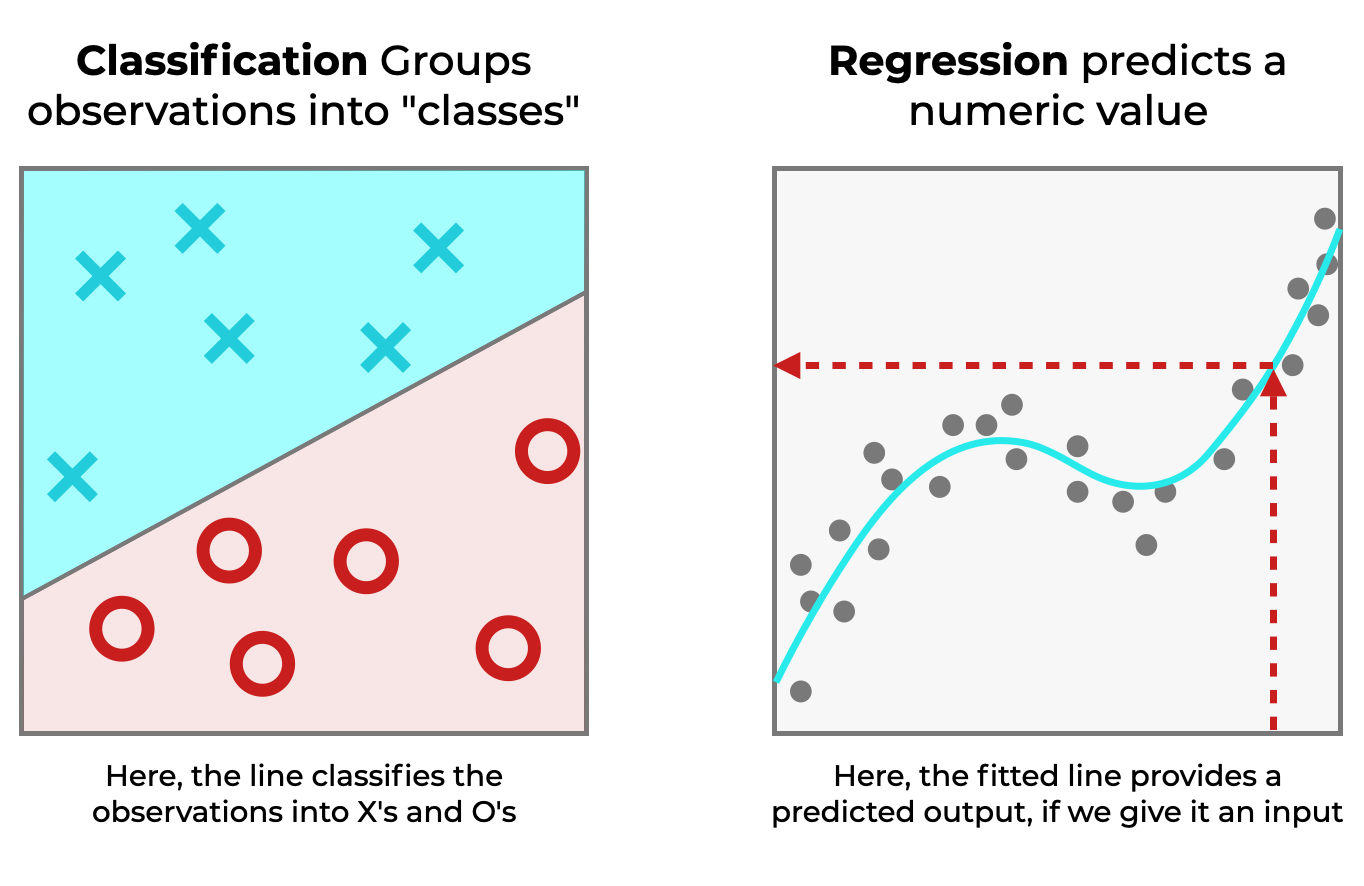
Regression or Classification
image source: Sharp Sight Labs
Supervised Learning vs Unsupervised Learning
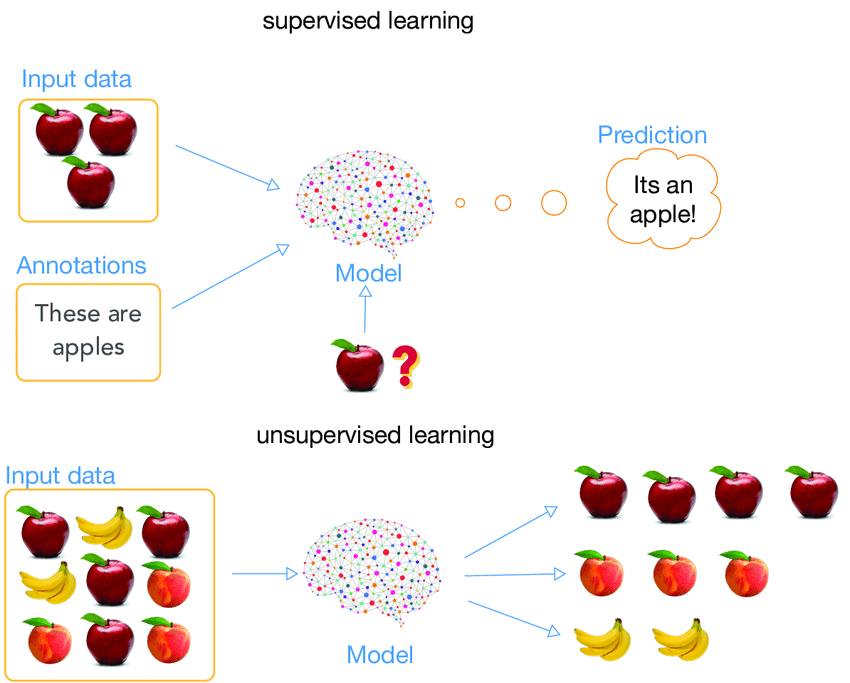
Supervised or Unsupervised
image source: Ma Yan, et al
Regularization
Loss function L(→β)=argmin→βN∑i=1(yi−β0−k∑j=1βjxij)2
L1 Regularization L(→β,λ)=argmin→β[N∑i=1(yi−β0−k∑j=1βjxij)2+λk∑j=i|βj|]
L2 Regularization L(→β,λ)=argmin→β[N∑i=1(yi−β0−k∑j=1βjxij)2+λk∑j=iβ2j]
Empirical Risk Minimization
We can approximate the expected risk over a loss function, data set, and hypothesis model h
E[L((→x,→y),h)] by taking the average over the training data
1nn∑i=1L((xi,yi),h) * formulas outlined by Professor Alexander Jung
Bias-Variance Tradeoff
Within a hypothesis class of similar modeling functions, we are concerned with the bias-variance tradeoff in model selection.
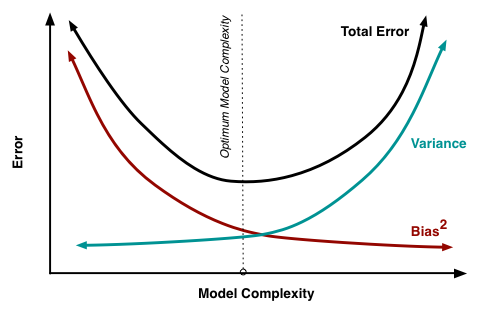
bias-variance tradeoff
image source: Scott Fortmann-Roe
Linear Foundations
“For more complex and high-dimensional problems with potential nonlinear dependencies between features, it’s often useful to ask:
- What’s a linear model for the problem?
- Why does the linear model fail?
- What’s the best way to add nonlinearity, given the semantic structure of the problem?